Big Data Approximating Control (BDAC)
|
Technical Resources:
BDAC Subtopics:
|
|
Overview of Big Data Approximating Control (BDAC)
Big Data Approximating Control (BDAC) is a new model-free approach to estimation and control problems. It eliminates separate steps for process identification, state estimation, and optimal control, directly synthesizing control actions based on a set of representative system trajectories. One core technology is approximate pattern matching, applying tools based on the “big data” set of technologies such as clustering. The goals are to improve advanced process control and estimation:
- Simplify the overall process of model identification, state estimation, and control
- Better address nonlinear systems
- Better address adaptation for process behavior and input changes
- Better address real time systems by reducing computing complexity and eliminating optimization methods
- Provide solutions for overdetermined or underdetermined control systems, and colinear data
- Incorporate feedforward as well as feedback control
- Systematically and efficiently handle missing data values
- Exploit rapid advances in “big data” and machine learning
Full details and examples are given in the paper Big Data Approximating Control (BDAC) - A new model-free estimation and control paradigm based on pattern matching and approximation . The paper was published in the Journal of Process Control (a publication from IFAC -- the International Federation of Automatic Control). A 5 minute audio-visual BDAC overview presentation is available at the publisher’s web page listed above. Unlike the paper, the presentation does not require a subscription to the journal. A version is also available on YouTube at https://www.youtube.com/watch?v=OF_fmmuY-rE&feature=youtu.be .
Only process input and output variables (such as measurements and controller outputs) that can be directly observed or calculated are considered. There is no usage of any mathematical model representing internal states. Each variable generates a time series, with values sampled periodically over finite time windows. The entire set of all time series values for each variable over a time window is called a trajectory. A trajectory for a given time window is assembled into a single long vector to facilitate pattern matching. Control includes both feedback and feedforward control.
The basic ideas for BDAC are simple and intuitive. At any point in time, recent past and current measurements are known for those inputs and outputs. The desired future values for the controlled process output variables are known - as setpoints of controllers (with possible ramping between setpoint changes). Future measured values for the independent process inputs are not known exactly, but can be predicted based on their current value, with confidence in those values decaying increasingly in the future. (If nothing else, assume they remain constant). Future process inputs that are controller outputs are not known. But a control goal for stability is that their incremental changes in the future should change towards zero. Future values for process outputs without setpoints are also not known, But a reasonable control goal is that their incremental changes in the future change towards zero, reflecting stable operation. So, values, predictions, or control goals are known for every variable in a trajectory centered around the current time. That is, there is a target trajectory, given the recent past and current values.
Suppose every possible feasible trajectory of input and output variables were stored within some small tolerance for each variable. This would be a massively large but finite set. Also suppose that the closest trajectory to the target could be retrieved quickly. Then the control problem would be solved—use that nearby trajectory to pick future control outputs. A set of control moves that worked well in this situation before is found, so use them again. This is control by approximate pattern matching.
There will always be approximation because of noise and unmeasured disturbances. Furthermore, target trajectories after a setpoint change will almost never be feasible, because they specify changes faster than the process could actually respond. Approximate pattern matching, rather than exact pattern matching, is required to find trajectories as close as possible to the target.
Such solutions were not practical in the past, partly due to limits in computer storage and speed of retrieval algorithms for nearest neighbors. But these limits are changing due to advances outside of process control: advances in hardware and advances in “big data” and machine learning. As an example, search engine query approximation looks for near matches in immense databases, where information is often coded with numeric attributes. Similarly, natural language understanding systems search vast databases for long sequences of phonemes.
BDAC is based on two independent processes: a training process to create and maintain a “training set” S of representative system trajectories, and an estimation & control process. The estimation & control process uses the training set, recent data, and targets, to determine future control actions and variable estimates. Either process can be stopped or started at any time. Continuing training (‘learning”) during control allows adaptive control.
BDAC data representation and the training process
One key idea is to focus on maintaining a representative set of system trajectories based on direct observations, rather than models. The representative trajectories are data for multiple variables sampled over a finite, sliding time window. There is no need for models or model identification steps, and there is no need for state variable representation. There is also no state estimator such as a Kalman filter, since estimation and control are calculated simultaneously, directly based on the representative data. Instead, BDAC stores trajectory vectors over finite time windows. At each time step, BDAC looks nh steps back in history and nh steps ahead. For instance, the graph below shows 5 variables plotted versus time ( 3 sensors and 2 controller outputs). (Click for full-sized image)
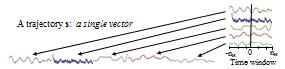 BDAC maps these 5 individual time series into one long vector called a trajectory. That allows the application of pattern matching techniques that look for approximate matches between two vectors. BDAC representation is covered in more detail in the section on BDAC system representation. BDAC maps these 5 individual time series into one long vector called a trajectory. That allows the application of pattern matching techniques that look for approximate matches between two vectors. BDAC representation is covered in more detail in the section on BDAC system representation.
The training process periodically acquires a new trajectory s. For each new trajectory, the training process performs time smoothing using Savitzky-Golay smoothing, rejects certain undesirable cases and outliers, and then performs “case filtering”. Case filtering combines new and existing close trajectories to further reduce sensor noise, to reduce the process noise introduced by unmeasured disturbances, and to adapt for process changes. Case filtering also reduces the amount of storage needed. The cases are stored as the rows si of a matrix S. The example below shows multiple trajectories for a 3-variable case. (Click for full-sized image)
 To support case filtering, an efficient new clustering technique called RTEFC (Real Time Exponential Filter Clustering, sometimes shortened to EFC) was created, focusing on real time needs. The cases (representative trajectories) are the centroids in the clustering technique. This is described in more detail in the section on Clustering and filtering in real time with RTMAC and RTEFC. To support case filtering, an efficient new clustering technique called RTEFC (Real Time Exponential Filter Clustering, sometimes shortened to EFC) was created, focusing on real time needs. The cases (representative trajectories) are the centroids in the clustering technique. This is described in more detail in the section on Clustering and filtering in real time with RTMAC and RTEFC.
The BDAC approximation problem
Another key idea in BDAC is control through approximate pattern matching. The idea is to choose a target trajectory starget at each time step, and find a close match among the set of all possible trajectories that would be feasible. That is, minimize the distance of the solution from the target, subject to a constraint that the solution is in (or close to)  , defined as the set of all feasible trajectories. The distance is based on a weighted Euclidean norm, as in MPC (Model Predictive Control). As in MPC, there are penalties for future deviations from setpoints and future changes in manipulated variables. But since BDAC also solves an estimation problem, there are also weights to penalize deviations of solutions from past sensor values and controller outputs. There are also weights to penalize future changes in sensors for process outputs without setpoints. , defined as the set of all feasible trajectories. The distance is based on a weighted Euclidean norm, as in MPC (Model Predictive Control). As in MPC, there are penalties for future deviations from setpoints and future changes in manipulated variables. But since BDAC also solves an estimation problem, there are also weights to penalize deviations of solutions from past sensor values and controller outputs. There are also weights to penalize future changes in sensors for process outputs without setpoints.
The BDAC approximation problem is stated formally as:
min || s - starget ||
subject to s in 
where  is the set of all feasible trajectories is the set of all feasible trajectories
 is an abstract set, not directly known. However, approximate solutions to the problem are obtained based on the examplars {si} that are the rows of the training data set S. The following are some approximate solutions: is an abstract set, not directly known. However, approximate solutions to the problem are obtained based on the examplars {si} that are the rows of the training data set S. The following are some approximate solutions:
- Approximate
 as all linear combinations of rows of S. Then a solution uses BDAC-O, which projects the target onto the row space of S using orthogonal decomposition. as all linear combinations of rows of S. Then a solution uses BDAC-O, which projects the target onto the row space of S using orthogonal decomposition.
- Approximate a solution as a linear or nonlinear combination of nearest neighbors of the rows of S. Two examples are BDAC-IDW (Inverse Distance Weighting) and BDAC-LSH (Locally Sensitive Hashing)
None of these solutions require an optimizer or other unknown amounts of iteration at each time step. The cited paper mostly covers BDAC-O.
The BDAC estimation and control process
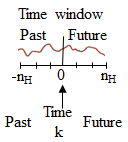 The stored trajectories represent examplars of a time window of 2nH + 1 time steps, with an index centered at 0. BDAC matches the current trajectory against the stored trajectories, with the current time step k lined up against index 0 in the stored trajectories. So, negative indices in the stored trajectories correspond to the past, and positive indices correspond to the future. At each time step, a target trajectory starget is created. Past values in starget are set based on past sensor readings and controller outputs. Targets for future values for the sensors are the setpoints. We don't know the future controller outputs. But we do know that that we want the incremental output changes over time to converge to 0 for stability. To facilitate pattern matching, the trajectories actually store incremental controller outputs for future values. The approximate pattern matching results in a trajectory that is close to the desired target, but feasible. The estimation and control process then extracts the desired controller output changes, along with any measured variable estimates of interest). So, estimation and control are accomplished in one step, replacing a Kalman filter and Model Predictive Control (MPC). The stored trajectories represent examplars of a time window of 2nH + 1 time steps, with an index centered at 0. BDAC matches the current trajectory against the stored trajectories, with the current time step k lined up against index 0 in the stored trajectories. So, negative indices in the stored trajectories correspond to the past, and positive indices correspond to the future. At each time step, a target trajectory starget is created. Past values in starget are set based on past sensor readings and controller outputs. Targets for future values for the sensors are the setpoints. We don't know the future controller outputs. But we do know that that we want the incremental output changes over time to converge to 0 for stability. To facilitate pattern matching, the trajectories actually store incremental controller outputs for future values. The approximate pattern matching results in a trajectory that is close to the desired target, but feasible. The estimation and control process then extracts the desired controller output changes, along with any measured variable estimates of interest). So, estimation and control are accomplished in one step, replacing a Kalman filter and Model Predictive Control (MPC).
BDAC is a form of moving horizon control analogous to MPC. It is based on a finite size time window, looking into the recent past and near future. At each time step, the entire desired trajectory is calculated, but control output is only implemented for the next time step. Then, at the next time step, new sensor data is collected, and the process is repeated.
The estimation and control process is formally stated as follows. For each time step k:
- Acquire past and current measurements at time step k
- Calculate the target trajectory starget[k] over the current time window
- Find s* solving or approximately solving the BDAC approximation problem
- Extract the manipulated variable increment du[k] for this time step from s* (along with any other desired estimates for past, present, or future)
- Apply typical control limits to du[k] and u[k] = u[k-1] + du[k]
- Send u[k] to the process
BDAC-O: An orthogonal decomposition approach to solving the BDAC approximation problem
BDAC-O is a solution for step 3 in the overall estimation and control process. The set  of all feasible trajectories is approximated as the set of all possible linear combinations of the representative trajectories {si} stored as the rows of the matrix S. BDAC-O solves the optimization problem by first constructing an orthonormal basis {ei} for the rows of S. Then the solution to the optimization problem is the orthogonal projection of the target starget onto the space spanned by the orthonormal basis vectors: of all feasible trajectories is approximated as the set of all possible linear combinations of the representative trajectories {si} stored as the rows of the matrix S. BDAC-O solves the optimization problem by first constructing an orthonormal basis {ei} for the rows of S. Then the solution to the optimization problem is the orthogonal projection of the target starget onto the space spanned by the orthonormal basis vectors:
s* =  < starget , ei > ei < starget , ei > ei
where the sum is over the orthonormal basis vectors indexed by i, and where <x1,x2> is the weighted inner product (dot product) between two vectors x1 and x2. The weighting factors are the same ones used in the definitions of norms and distances.
This single projection operation is the core of the BDAC-O estimation and control algorithm. By finding the closest vector to the feasible space, BDAC balances the closeness of past and current sensor data, closeness to desired future targets or prediction, and the size of the incremental control outputs. It is important to note that although BDAC-O is a linear method, the trajectories already incorporate all the observed nonlinearities, and all higher-order dynamics that might be lost in model-based controls that force a fit to a low order model. BDAC-O can be thought of as doing interpolation between those nonlinear cases.
Other solutions to the BDAC approximation problem
Other solutions to the BDAC approximation problem should provide better approximations for highly nonlinear systems, with more reliance on just the nearest neighbors of the target. These methods need further research. Work to date has focused on BDAC to demonstrate the overall process, and not depend as much on having extensive local data for all operations regions. The other approaches include Inverse Distance Weighting (IDW) and Locally Sensitive Hashing (LSH). Inverse Distance Weighting is a nonlinear multivariable interpolation method originally developed for image processing. Hashing is a technique widely used in computer systems for cryptography, and to quickly access items such as vectors, based on a hash value. A hash value is simply a short code, so that a high dimensional search problem is reduced to a much smaller one. But conventional hashing has no locality. That means that two nearby vectors will have completely different hash codes. So, conventional hashing would be unusable for searches to achieve approximate pattern matching. But LSH allows retrieval of nearby vectors based on their hash code. It was developed for search engines, as an efficient way to search large databases for near matches.
Benefits of the new paradigm
Nonlinear systems
Each stored trajectory already incorporates all nonlinearities along that trajectory. Solutions by BDAC can be thought of as interpolating between these trajectories. So, with enough stored trajectories, even the approximations between trajectories will still be very close to the real system behavior. Clustering separates different operating regions and modes, so that nonlinearities over a wide range of conditions are remembered and used. For severe nonlinearities, the “kernel trick” can be used. The idea is to add extra variables to capture the nonlinear behavior. This basic idea has been around for a long time. For instance, linear regression is a purely linear method, like BDAC-O. However, extra calculated data is included, such as squared and cubed values so that polynomial curve fits can be done. With just minimal engineering insight, many nonlinearities are known. For instance, an exponential function of temperature captures the Arrhenius reaction rate factor for chemical reactions. Relations such as square root or square are common in representing flow and pressure behavior. Energy balances and component material balances contain products of flow and temperature or composition. These extra terms are simply included as pseudomeasurements. This approach works well with BDAC, but is not as useful for conventional control methods such as MPC (Model Predictive Control). With those methods, there still needs to be effort expended to derive linearized models, either analytically or empirically. Nonlinear optimization packages are also generally needed.
Avoid problems with approximating complex behavior with overly-simplified models
Model-based controls may make assumptions such as low-order models or ignoring time delays, besides sometimes assuming linearity. But all of these effects are captured in the observed trajectories, without forcing model assumptions.
Adaptation
Adaptation occurs naturally simply by running the training process, whether control is active or not. Learning can be done while in manual modes, closed loop control by other control systems, or closed loop control by BDAC.
Simplicity
Without models, there is no need for a model identification step. There is no need to rebuild models when adaptation is desired. There is no need for a state estimator such as a Kalman filter. There is no need for linearization, either analytically or empirically. There is no need for an optimization package. The method is simple. For instance, the heart of BDAC-O is just a projection of the target onto the training data set.
Efficiency and predictable timing for “hard real time
The training process with RTEFC is efficient and non-iterative, as are the control calculation steps. This means that the worst case computing time is known by experiment. “Hard real time” systems can be addressed: systems where computation must be complete within a time limit.
Handling dimensionality issues such as overdetermined or underdetermined systems, as well as colinear data
BDAC provides estimation and control when the control system has the number of controller inputs with targets less than, equal to, or greater than the number of manipulated variables. The controller makes a best effort to achieve the targets, based on the weighting factors. Similarly, having extra measurements that may be colinear is not a problem, unlike in some control approaches. The redundancy of information is exploited, essentially doing a form of dynamic data reconciliation, again based on the weights assigned to each measurement. Feedforward control is incorporated as well as feedback control.
Other benefits
Soft sensing can easily be accommodated. This can be used to replace missing, slowly, or irregularly sampled sensors, such as analyzers. Some problems in MPC systems such as collinearity are not an issue. BDAC works with underdetermined or overdetermined systems. Also, pattern approximation isn’t restricted to just numerical variables. For instance, there could be binary or symbolic variables for operating modes, faults, etc. Finally, BDAC can exploit rapid advances being made in machine learning and “big data”. For instance, improved clustering techniques that will support rapid recovery and use of local data in extremely nonlinear systems.
Simulation studies
BDAC-O and BDAC-IDW were tested on several simulated processes. For details, see the section on BDAC simulation results.
(Additional material to follow at a later date)
Copyright 2017-2020, Greg Stanley
(Return to Technical Resources)
|