BDAC simulation results
This page examines simulation results for several BDAC examples. It is a part of
BDAC - Big Data Approximating Control
Overview of simulation studies
BDAC-O and BDAC-IDW were tested on several simulated processes. Although BDAC does not use state variable representation, the overall framework and simulator use state space representation for convenience in modeling. In all cases, random noise was added to measurements. Only a few cases are reviewed here. A larger selection, and more details, are available in the first published BDAC paper. Detailed simulation reports are also available there as supplementary materials.
The simulated processes
Simulations included simple systems such as a first order lag plus dead time, with and without feedforward. Another simple example was an integrating process with dead time. The examples also included more complex nonlinear multivariable systems. One example used 4 cross-connected first-order lags with dead times, with nonlinearities in lag times and gains. The nonlinearities were representative of some types typically encountered in process control: lag depending on volume and flowrate (V/f), and diminishing heat transfer gain with temperature approach. That example uses 6 measurements total, including 2 linearly dependent measurements, and has 2 manipulated variables. The more well-known example of a standard “quadruple tank” control system was also simulated. It has 4 state variables, 2 manipulated variables, and 2 measured states (two of the levels). The nonlinearities are due to the exit flows depending on the square root of tank levels. Due to the unusual arrangements of the tanks, the system is known to be very difficult to control. In particular, the system operating conditions can make a transition between nonminimum phase and minimum phase operation.
Types of tests
The following types of tests were conducted:
- Regulatory control (load disturbances) and setpoint changes
- Adaptation to cyclic or sustained unmeasured load disturbances/process changes
- Noise level
- Simultaneous learning and control while expanding beyond previously-known operating conditions
- Estimating missing sensor values
- Automated testing while in manual, BDAC control, or other control
- Comparisons with PID for SISO cases with and without feedforward
- Comparisons to a multi-model MPC for the quadruple tank example
Testing follows the approach to be used when installing BDAC
The tests followed the sequence of steps that would be used when installing in a real system. BDAC starts with no information. It first collects information passively, monitoring the system, whether some or all of the previous controllers were in manual modes or active. Then, BDAC starts providing PRBS (Psuedo Random Binary Sequence) test signals simultaneously to each manipulated variable output, without attempting control unless basic control is needed for stability. For instance, for the integrating process, the PRBS test signal is superimposed on top of proportional control. Then BDAC starts full automatic control (usually one output at a time). In all cases, BDAC continues learning regardless of any control modes. In all but one of the examples, BDAC used nH = 10, so it looked back and forward 10 time samples from the current value, for a total of 21 values.
The test results report format
The first group of plots shows variables vs. time on the x-axis. The variables are the state variables x, the disturbance variables d, the manipulated variables u, and the measured variables y. In some cases, comparisons to single-variable PID controls are shown for comparison. The “BDAC y estimates” plot shows how effectively BDAC estimates measurements without a Kalman filter. The “BDAC smoothed variables” plot shows the effects of Savitzky-Golay smoothing for the separate varialbes prior to other BDAC calculations, independent of any other estimation or control.The “BDAC new trajectory proximity to training cases during training” shows the growth and updating of the training cases over time. It plots the index to the case closest to newly-observed trajectories during training, with artificial values for several reasons for rejected data. “BDAC traget proximity to training cases during estimation and control” shows the closest training case to the target, and the associated distance. It is based on the latest data, unlike the previous training information plot. “BDAC norms” plots the norms versus time for the target and its “infeasibility”, which is the distance to the feasible set. Also, a semi-norm for weighted setpoint error is plotted. “BDAC target weighting factors in training set” plots the spectral coefficients (weighting factors for the projection of the target onto the feasible space in terms of the orthogonal basis vectors), for the target versus time. In the case of BDAC-IDW, it just shows weighting factors for each case when the approximated target is calculated.
The second group of plots is not time-based. “BDAC training data cases” plot the training set and the orthonormalized version. The x axis represents the vector index into each trajectory.
After the plots, there is an event log, listing significant events such as controller mode changes, setpoint changes, and so on. There is also a training report, controller performance reports, and controller configuration information.
Example: First order lag plus dead time, with feedback control and feedforward
BDAC-O is compared to a PID controller for a simulated first order plus dead time process. The PID controller is already tuned, but BDAC starts with no information. The process gain is 1.0; the time constant is 2.0; and the dead time is 1.5. There is one measured process input disturbance d0 used for feedforward control in BDAC, along with an unmeasured disturbance d1. The manipulated variable u0 is used for feedback control of y0, the single process output measurement. The PID controller was manually tuned for stable but good responses for load changes or setpoint changes, with a gain of 1 and integral time of 5, and no derivative action. Proportional action is on the process variable rather than setpoint error, to avoid overshoot in response to setpoint changes (typical practice for process industry PID controllers unless they are the secondary controller in a cascade control loop).
The same unmeasured and measured disturbances are sent to identical, parallel processes for the PID controller and the BDAC controller, and setpoints are set the same at all times. The testing included setpoint as well as load changes introduced through the unmeasured disturbance. A plot of the key variables with annotations follows. (Click for full sized image).
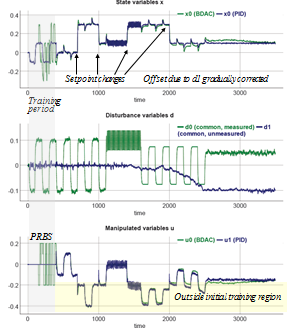 For more details, and to see some of the other plots referenced later, see the full report for a similar simulation run. Measured value y0 is just x0 plus added random noise; y0 is not shown here. The simulation starts out with both controllers in manual mode, so that the effects of the unmeasured disturbance can be seen. The measured disturbance variable d0 starts at 0 plus random noise, until time 21 when it switches to a filtered noisy large square wave. The unmeasured disturbance d1 starts as a small-amplitude filtered square wave with a cyclically varying period, plus random noise. At time 150, BDAC starts test mode (training period) with a PRBS controller output. This continues until time 400, when both the BDAC and PID controls switch to automatic control with setpoints of 0. Setpoints and disturbance variables change several times, taking the system into new operating regions. At time 1400, in addition to a setpoint change, unmeasured disturbance d1 starts a random walk with a downward bias, eventually drifting down to −0.1. That is a transition from one sustained unmeasured disturbance to another. For more details, and to see some of the other plots referenced later, see the full report for a similar simulation run. Measured value y0 is just x0 plus added random noise; y0 is not shown here. The simulation starts out with both controllers in manual mode, so that the effects of the unmeasured disturbance can be seen. The measured disturbance variable d0 starts at 0 plus random noise, until time 21 when it switches to a filtered noisy large square wave. The unmeasured disturbance d1 starts as a small-amplitude filtered square wave with a cyclically varying period, plus random noise. At time 150, BDAC starts test mode (training period) with a PRBS controller output. This continues until time 400, when both the BDAC and PID controls switch to automatic control with setpoints of 0. Setpoints and disturbance variables change several times, taking the system into new operating regions. At time 1400, in addition to a setpoint change, unmeasured disturbance d1 starts a random walk with a downward bias, eventually drifting down to −0.1. That is a transition from one sustained unmeasured disturbance to another.
The BDAC controller takes some time to learn the new conditions outside the original training region, but otherwise mostly matches the PID control. 23 cases are learned during the initial manual and testing period. There is overshoot at the first SP change to a new region at time 700, which coincided with a large d0 change. This corrects itself while under control for subsequent upsets, as 7 new training cases are added and previous cases are updated, as can be seen in the “new trajectory proximity to training cases” graph. When the unmeasured disturbance starts drifting at time 1600, some offset occurs, but is nearly corrected by time 2000. The “BDAC norms” plot shows that these offsets observed near time 2000 occur near a steady state with little infeasibility error, so that adaptation is required to correct the offset. The “BDAC y estimates” graph shows that BDAC underestimates changes in the values of measurements y0 until enough training cases are acquired to adequately represent the feasible subspace. By the end of the training period, the estimates track the measurements. After that, the “BDAC norms” plot shows that the main deviations and infeasibilities occur mainly in short bursts due to setpoint changes or major process disturbances.
By the end of the simulation, the number of training cases has increased to 32. Also, as can be seen by the “new trajectory proximity” graph, adaptation (updating of old cases) was required to gradually reduce the offset introduced because of the drift in d1. The slow decrease in offset reflects the high RTEFC filter constant at 0.998, which is equivalent to a “time constant” of about 500. From the BDAC controller report, the controller requested updating by the trainer 1020 times to reduce offset.
The randomness of PRBS testing can lead to different results. Often, there is some sluggishness and offset when initially entering new regions. This is corrected eventually by adaptation, and by the partial integral action discussed in the original paper. However, there are times when BDAC-O went unstable when entering a new region. Some work is still needed on maintaining and enlarging the training set, and guaranteeing stability.
BDAC is not proposed as a replacement for PID. Its use will likely be reserved for more complex multivariable situations. This example merely demonstrated dealing with typical control issues such as feedback, feedforward, lags, dead times, noise, unmeasured disturbances, adaptation to account for sustained unmeasured disturbances, learning starting from no process knowledge, learning while in manual or automatic control, PRBS testing, and setpoint and load changes.
Variations of this example are included in the original paper, including higher noise levels, and the loss of the main sensor y0 (measured x0).
Example: The Quadruple tank process
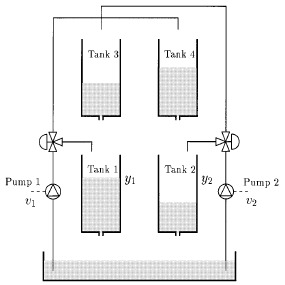 The quadruple tank process was developed by Johansson and Nunes for training and for use in controller testing, as described in a 1998 paper and a 2000 paper. It has been a popular controls testbed because it has nonlinear (square root) elements typical of process control applications, and also allows transition from minimum phase operation to nonminimum phase operation due to the unusual tank configuration. The nonminimum phase operation in particular is very difficult to control. Settling times for typical controls are ten times longer than in the minimum phase case. The quadruple tank process was developed by Johansson and Nunes for training and for use in controller testing, as described in a 1998 paper and a 2000 paper. It has been a popular controls testbed because it has nonlinear (square root) elements typical of process control applications, and also allows transition from minimum phase operation to nonminimum phase operation due to the unusual tank configuration. The nonminimum phase operation in particular is very difficult to control. Settling times for typical controls are ten times longer than in the minimum phase case.
The adjacent diagram from the original paper shows the process with its 4 tanks, all with gravity-based tank outflows proportional to the square root of level. The process inputs are pump flows, set by voltages v1 and v2 as manipulated variables in the control system. The process states are the 4 levels, but only the two lower tank levels are measured, translated to voltages y1 and y2. The upper tank 3 feeds the lower tank 1 by gravity feed, and the upper tank 4 feeds the lower tank 2 similarly. The manually-set 3-way valves are used to change the behavior of the system. They split the two pump flows between their adjacent lower tanks and the opposite upper tanks. Increasing the flow to the upper tanks increases the control difficulty, leading to nonminimum phase operation. The 3-way valve settings are unmeasured in the control system, so changes in their settings during operation can be thought of as process changes or unmeasured disturbances.
Many approaches have been tried for controlling this system. A test sequence defined in a 2007 paper by Kuure-Kinsey and Bequette was followed.
A portion of a simulated test run is shown in the annotated graphs below (Click for full-sized image).
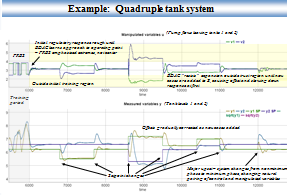 Training runs up until time 6000 seconds, using simultaneous PRBS process inputs for the two pump flows (as voltages v1 and v2). Both manipulated ouputs are switched to automatic control at time 6000 seconds. The system settles, but takes a little time because the controller needs to learn a few more cases to learn the operating point. (The PRBS testing emphasized high and low values around the setpoint). This is at a standard minimum phase operating point identified in the Johansson papers. Starting at time 8600, a single setpoint change is introduced, then returned to the base case. Some small high frequency oscillation is visible in v1, along with an initially slow response. This is due to some BDAC logic to slow down excursions into new operating areas. Then a series of 3 tests make simultaneous changes to both setpoints. With the earlier step tests, there is some offset because the manipulated or controlled variables (or both) go outside of their training range. But over time, more cases are learned, and the offsets are eliminated. At time 12000, a severe upset is introduced: the 3-way valve settings are changed to force nonminimum phase operation. The controls have to learn more cases, but then stabilize at the new operating point. Training runs up until time 6000 seconds, using simultaneous PRBS process inputs for the two pump flows (as voltages v1 and v2). Both manipulated ouputs are switched to automatic control at time 6000 seconds. The system settles, but takes a little time because the controller needs to learn a few more cases to learn the operating point. (The PRBS testing emphasized high and low values around the setpoint). This is at a standard minimum phase operating point identified in the Johansson papers. Starting at time 8600, a single setpoint change is introduced, then returned to the base case. Some small high frequency oscillation is visible in v1, along with an initially slow response. This is due to some BDAC logic to slow down excursions into new operating areas. Then a series of 3 tests make simultaneous changes to both setpoints. With the earlier step tests, there is some offset because the manipulated or controlled variables (or both) go outside of their training range. But over time, more cases are learned, and the offsets are eliminated. At time 12000, a severe upset is introduced: the 3-way valve settings are changed to force nonminimum phase operation. The controls have to learn more cases, but then stabilize at the new operating point.
Kuure-Kinsey and Bequette emphasize that linear controllers cannot handle this type of shift in the phase behavior of the process. The solution in the paper cited above was with MMPC, building a bank of linear MPC models ahead of time for each operating point, and also carefully tuning the associated Kalman filter. Generally, the BDAC response was slower than the MMPC results except at the change in phase behavior. But, BDAC is much simpler, and did not require separate training, model building, and Kalman filter tuning ahead of time.
Copyright 2017-2020, Greg Stanley
(Return to BDAC - Big Data Approximating Control )
|